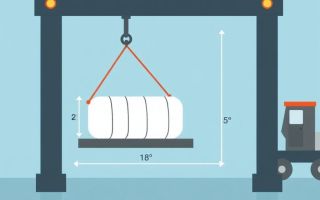
Wenn ein schweres Stück Fracht, eine Maschine oder ein unhandliches Bauteil in die Luft gehoben werden muss, entscheidet nicht nur das Nenngewicht über die Sicherheit — entscheidend ist, wie diese Last verteilt ist und wo ihr Schwerpunkt liegt. In diesem Artikel entflechten wir die oft einschüchternde Sprache von Kräften, Momenten und Schwerpunkten in klare, handhabbare Schritte. Sie lernen, wie man die zu hebende Last berechnet, wie der Schwerpunkt (centre de gravité) bestimmt wird, warum er die Art des Hebens beeinflusst und wie man anhand einfacher Rechnungen und Tabellen eine sichere Hebeanordnung plant. Der Ton ist praxisnah und anschaulich: viele Beispiele, klare Formeln, nummerierte Checklisten und Tabellen helfen Ihnen, beim nächsten Hebevorgang sicher und kompetent zu handeln.
Warum Lastberechnung und Schwerpunktberechnung so wichtig sind
Bevor ein Haken, eine Kette oder ein Hebegeschirr angesetzt wird, muss klar sein, welche Last tatsächlich angehoben wird. Gewicht allein ist nur die halbe Wahrheit: der Schwerpunkt bestimmt, wie die Last sich verhält. Wenn der Schwerpunkt nicht zentral unter den Hebepunkten liegt, kann die Last kippen, drehen oder unerwartet hohe Kräfte auf einzelne Anschlagmittel erzeugen. Ein falscher Hebevorgang kann daher nicht nur Schäden am Lastgut bedeuten, sondern Leben gefährden.
Die Gesetze der Statik sind hier nicht optional, sie sind die Grundlage jeder sicheren Hebeplanung. Die Summe der vertikalen Kräfte muss gleich Null sein (bei ruhender Last) und die Summe der Momente um einen beliebigen Punkt ebenfalls. Das klingt kompliziert, lässt sich aber systematisch zerlegen und in einfache Formeln und Schritte fassen. In den folgenden Abschnitten gehen wir genau auf diese Schritte ein, geben praktische Faustregeln und durchspielen Beispiele — vom einfachen Kasten bis zur komplexen unregelmäßigen Maschine.
Grundbegriffe: Kraft, Moment und Schwerpunkt (centre de gravité)
Bevor wir rechnen, definieren wir die Begriffe präzise, aber leicht verständlich. Die Masse (m) multipliziert mit der Erdbeschleunigung (g ≈ 9,81 m/s²) ergibt die Gewichtskraft (W = m·g). Diese Kraft muss vom Hebezeug ausgeglichen werden. Der Schwerpunkt ist der Punkt, an dem die gesamte Masse so konzentriert angenommen werden kann, dass die Lage der Last durch eine einzige Resultierende beschrieben ist. Bei ideal symmetrischen Körpern liegt der Schwerpunkt in geometrischem Zentrum, bei unregelmäßigen Körpern verschiebt er sich in Richtung schwerer Anbauteile.
Das Moment (Drehmoment) entsteht, wenn eine Kraft nicht durch den betrachteten Punkt (z. B. einen Hebepunkt) wirkt, sondern einen Hebelarm hat. Das Moment ist das Produkt aus Kraft und Hebelarm (M = F·d) und entscheidet darüber, ob die Last kippt oder stabil bleibt. Beim Heben gilt: Summe der vertikalen Kräfte = 0 und Summe der Momente um den Schwerpunkt (oder einen beliebigen Punkt) = 0.
Werkzeuge und Hilfsmittel für sichere Berechnungen
Wer ernsthaft heben will, sollte drei Dinge dabei haben: ein paar einfache Werkzeuge, Messmethoden und klare Tabellen für schnelle Entscheidungen. Messen Sie Abstände zwischen Hebepunkten und zum vermuteten Schwerpunkt mit einem Maßband oder Laserentfernungsmesser. Verwenden Sie eine Waage (z. B. eine Kranwaage) für das tatsächliche Wiegen. Ein Linienlaser kann helfen, Fluchten und Symmetrien zu prüfen. Ein Notizblatt oder eine einfache Excel-Tabelle reduzieren Rechenfehler.
Praktische Hilfsmittel:
- Messband/Laser-Entfernungsmesser
- Kranwaage oder Federwaage zum Wiegen
- Inklinometer (Winkelmesser) für Anschlagwinkel
- Skizzenpapier oder digitales Zeichentool
- Herstellerdatenblatt der Anschlagmittel (WLL/Tragfähigkeit)
Schritt-für-Schritt-Anleitung: So berechnen Sie Last und Schwerpunkt
Wir gehen Schritt für Schritt vor — von der Bestimmung des Gewichts bis zur Berechnung der einzelnen Spannungen in den Anschlagmitteln.
Schritt 1: Masse und Gewicht bestimmen
Zuerst das Offensichtliche: Wie viel wiegt das Objekt? Wenn möglich, wiegen Sie es. Falls nur die Masse in kg angegeben ist, multiplizieren Sie m mit der Erdbeschleunigung g, um die Gewichtskraft W in Newton zu erhalten: W = m · g. Für schnelle Abschätzungen können Sie mit kg arbeiten, wenn Sie später mit Lasten in Tonnen oder kgf rechnen — achten Sie nur auf konsistente Einheiten.
Schritt 2: Lage des Schwerpunkts schätzen oder messen
Bei präziser Arbeit bestimmen Sie die Koordinaten des Schwerpunkts: x, y, z relativ zu einem definierten Bezugspunkt. Bei regelmäßigen Formen (Quader, Zylinder) gibt es bekannte geometrische Mittelpunkte. Bei zusammengesetzten oder unregelmäßigen Lasten teilen Sie das Objekt in einfache Teile, berechnen die Schwerpunkte der Teile und verwenden die gewichtete Mittelwertformel:
x_CG = (Σ m_i·x_i) / Σ m_i
y_CG = (Σ m_i·y_i) / Σ m_i
z_CG = (Σ m_i·z_i) / Σ m_i
Schritt 3: Hebepunkte und Geometrie festlegen
Notieren Sie die Positionen der Hebepunkte relativ zum Bezugspunkt und zum Schwerpunkt. Skizzieren Sie die Anordnung maßstäblich.
Schritt 4: Gleichgewichtsbedingungen anwenden
Für vertikale Hebevorgänge gilt:
ΣF_v = 0 → ΣT_i = W (Summe der Spannungen/Tensions in den Anschlagmitteln = Gewichtskraft)
ΣM = 0 → Für horizontale Ebenen: z. B. Σ(T_i·x_i) = W·x_CG , je nach gewähltem Bezugspunkt.
Bei zwei Anschlagpunkten in einer Linie: T1 + T2 = W und T1·x1 = T2·x2 (x1, x2 sind Abstände vom Schwerpunkt). Daraus ergeben sich T1 = W·x2/(x1+x2) und T2 = W·x1/(x1+x2).
Schritt 5: Winkeleffekte berücksichtigen
Wenn Anschlagmittel nicht vertikal sind, erhöht sich die Zugkraft. Ist α der Winkel zur Vertikalen, dann ergibt sich die vertikale Komponente einer Zugkraft T als T·cos(α). Für zwei symmetrische Schlingen mit Winkel α zur Vertikalen gilt: T = W / (2·cos(α)). Deshalb steigt die Belastung mit zunehmendem Winkel deutlich an.
Schritt 6: Sicherheitsfaktoren und Vergleich mit WLL
Vergleichen Sie die berechneten Spannungen mit den Working Load Limits (WLL) der verwendeten Anschlagmittel und Haken. Achten Sie auf Sicherheitsfaktoren, Inspektionsstatus und eventuelle Schrägstellung von Ketten/Seilen.
Schritt 7: Lastprobe und kontinuierliche Beobachtung
Führen Sie, wenn möglich, eine Anprobe durch: kurz anheben, wenige Zentimeter, prüfen ob die Last stabil hängt und keine überraschende Schräglage zeigt. Beobachten Sie während des gesamten Hebevorgangs.
Beispiel 1 — Einfacher Kasten, zwei Hebepunkte (vollständige Rechnung)
Nehmen wir einen praxisnahen Fall: Ein quaderförmiger Kasten hat die Masse m = 2000 kg. Er soll mit zwei Anschlagpunkten gehoben werden, die 1,0 m auseinander liegen. Der Schwerpunkt liegt nicht mittig, sondern 0,2 m vom linken Hebepunkt (dort ist er näher), also 0,8 m vom rechten Hebepunkt. Berechnen wir die Lasten in den beiden Anschlagpunkten.
Erste Rechnung: Gewichtskraft
W = m·g = 2000 kg · 9,81 m/s² = 19.620 N (ca. 19,62 kN)
Gleichgewichtsbedingungen:
T1 + T2 = W
T1·x1 = T2·x2 , wobei x1 = 0,2 m (Abstand vom Schwerpunkt zum linken Hebepunkt) und x2 = 0,8 m (zum rechten).
Lösung:
T1 = W·x2 / (x1 + x2) = 19.620 N · 0,8 / 1,0 = 15.696 N
T2 = W·x1 / (x1 + x2) = 19.620 N · 0,2 / 1,0 = 3.924 N
Interpretation: Das linke Anschlagmittel trägt ca. 15,7 kN, das rechte 3,9 kN. Wenn die Anschlagwinkel nicht vertikal sind, sind diese Werte durch den Divisor cos(α) weiter zu multiplizieren. Besonders wichtig: Das rechte Anschlagmittel ist deutlich geringer belastet, was bei der Auswahl und Inspektion der Hardware berücksichtigt werden muss.
Tabelle 1: Beispieleintrag — Vertikale Lastverteilung bei zwei Hebepunkten
| Parameter | Wert |
|---|---|
| Masse | 2000 kg |
| Gewichtskraft W | 19.620 N |
| Abstände zum Schwerpunkt (links/rechts) | 0,2 m / 0,8 m |
| Spannung T1 (links) | 15.696 N (≈ 1.600 kgf) |
| Spannung T2 (rechts) | 3.924 N (≈ 400 kgf) |
Beispiel 2 — Mehrere Anschlagpunkte, Berechnung des Schwerpunkts
Bei komplexen Lasten zerlegen wir die Struktur in Teilmassen. Ein typisches Beispiel ist eine Maschine mit einem schweren Motorblock auf einer Seite und leichteren Anbauteilen auf der anderen. Wir berechnen die Schwerpunkte der Teilmassen und dann den Gesamt-Schwerpunkt mittels gewichteter Mittelwerte.
Angenommen:
Teil A (Motor): m1 = 600 kg, x1 = 0,5 m (vom Bezugspunkt)
Teil B (Gehäuse): m2 = 900 kg, x2 = -0,2 m
Teil C (Zubehör): m3 = 200 kg, x3 = 0,1 m
Gesamtkraft:
m_total = 600 + 900 + 200 = 1.700 kg
Schwerpunkt x:
x_CG = (m1·x1 + m2·x2 + m3·x3) / m_total
x_CG = (600·0,5 + 900·(-0,2) + 200·0,1) / 1700
x_CG = (300 – 180 + 20) / 1700 = 140 / 1700 ≈ 0,08235 m
Der Schwerpunkt liegt also etwa 8,2 cm auf der positiven Seite des Bezugspunkts — eine wertvolle Erkenntnis, um Hebepunkte so zu wählen, dass die Verteilungsungleichheit minimiert wird.
Winkeleffekte und die berühmte cos(α)-Beziehung
Viele Hebefehler entstehen durch zu flache Anschlagwinkel. Der Effekt ist nicht linear: bereits bei 30° zur Vertikalen erhöht sich die Zugkraft deutlich. Definieren wir α als den Winkel zwischen dem Anschlagmittel und der Vertikalen. Die vertikale Komponente T_v einer Kraft T ist T_v = T·cos(α). Für symmetrische Systeme mit zwei Anschlagmitteln gilt daher:
T = W / (2·cos(α))
Wenn α = 0° (vertikal), dann cos(0)=1 und T = W/2. Wenn α = 30°, cos(30°)≈0,866 => T ≈ W / (2·0,866) ≈ 0,577·W ≈ 1,155·(W/2). Das heißt: jede Schlinge trägt ~15,5 % mehr als bei vertikaler Belastung. Bei 60° zur Vertikalen aber cos(60)=0,5 und T = W/(2·0,5)=W, also jede Schlinge würde das gesamte Gewicht tragen — katastrophal, wenn die Schlinge nur auf halb so viel ausgelegt ist.
Tabelle 2: Winkel-Faktoren (α = Winkel zur Vertikalen)
| α (°) | cos(α) | Multiplikator für T (pro Schlinge bei 2 Schlingen) |
|---|---|---|
| 0 | 1,000 | 0,5 |
| 15 | 0,966 | 0,517 |
| 30 | 0,866 | 0,577 |
| 45 | 0,707 | 0,707 |
| 60 | 0,500 | 1,000 |
Diese Tabelle (Tabelle 2) zeigt eindrücklich, warum flache Winkel zu vermeiden sind. Bei 60° ist die Belastung pro Schlinge doppelt so hoch wie bei vertikaler Belastung eines symmetrischen Zweischlagers.
Lastverteilung bei mehreren Punkten — Matrizen und Momentengleichungen
Bei mehr als zwei Anschlagpunkten ist das Prinzip dasselbe, es wird nur algebraisch umfangreicher. Für n Anschlagpunkte ergeben sich n Gleichungen: eine für die Summe der vertikalen Kräfte und n-1 für die Momente um unabhängige Achsen. In der Praxis lassen sich für viele industrielle Anwendungen vereinfachte Formeln verwenden oder man nutzt Tabellen/Software.
Die Matrixgleichung lautet im Kern:
A·T = b
wobei T der Vektor der unbekannten Spannungen ist, A die Matrix der Hebelarme und cos(α)-Faktoren und b der Resultierende aus Gewichtskraft und Momenten. Für den praktischen Einsatz genügt häufig die Lösung per Taschenrechner oder einfache Excel-Tabellen.
Sicherheitsfaktoren, Normen und Verantwortung
Berechnungen sind nur so gut wie ihre Sicherheitsannahmen. Verwenden Sie nur Anschlagmittel mit bekanntem WLL und gültigen Prüfungen; berücksichtigen Sie Alter, Schäden, Temperatur und chemische Einflüsse. Typische Sicherheitsmaßnahmen umfassen:
- WLL der Schlingen/Haken mindestens 25–50 % über der berechneten Last (abhängig von Risiken) — genaue Vorgaben sind normativ geregelt.
- Eigengewicht von Anschlagmitteln und Umlenkern berücksichtigen.
- Dynamische Effekte (Ruck, Beschleunigung) durch Faktor oder Prüfplan abdecken.
- Regelmäßige Inspektion: Sichtprüfung vor jedem Einsatz.
- Qualifizierte Personen für Planung und Freigabe.
Hinweis: Spezifische Sicherheitsfaktoren und Vorschriften (z. B. EN-, ISO- oder OSHA-Standards) sind zu beachten. Diese können je nach Land, Branche und Art des Anschlagmittels variieren. Konsultieren Sie stets die geltenden Normen und die Angaben des Herstellers.
Checkliste vor dem Heben (nummeriert und kurz)
Vor jedem Hebevorgang sollten Sie systematisch vorgehen. Diese nummerierte Checkliste hilft, nichts Wichtiges zu übersehen:
- Wiegen: Ist das tatsächliche Gewicht bekannt oder geschätzt? Wenn möglich, wiegen.
- Schwerpunkt: Lage bestimmen oder schätzen; evtl. Markierung anbringen.
- Hebepunkte: Positionen, Abstand und Tragfähigkeit prüfen.
- Anschlagwinkel: Winkel messen, möglichst vertikal halten.
- Anschlagmittel: Zustand, Kennzeichnung, WLL kontrollieren.
- Lastverteilung berechnen: Spannungen für jedes Anschlagmittel ermitteln.
- Sicherheitsfaktoren anwenden und geeignete Reserve einplanen.
- Testheben: Kurz anheben, Stabilität prüfen und ggf. anpassen.
- Arbeitsbereich sichern: Personen entfernen, Fallbereiche freihalten.
- Dokumentation: Berechnungen und Freigabe durch verantwortliche Person sichern.
Weitere praktische Beispiele: Ein schief hängender Kessel

Ein Kessel mit unregelmäßiger Wanddicke hat seinen Schwerpunkt um 0,4 m vom geometrischen Zentrum verschoben. Er soll mit drei Hebepunkten an einem Dreieck gehoben werden. Die Lösung erfolgt durch Aufzeichnung der Hebepunktkoordinaten und Lösung der Gleichungen ΣT_i = W, Σ(x_i·T_i) = W·x_CG und Σ(y_i·T_i) = W·y_CG. In der Praxis setzt man dies in eine kleine Excel-Lösung um: die Matrixgleichung A·T = b wird gelöst (z. B. mit Excel-Funktionen oder einem numerischen Solver). Anschließend verifiziert man die Ergebnisse durch ein Testheben.
Tabelle 3: Typische Wichtige Zahlen und Faustregeln
| Thema | Faustregel / Wert |
|---|---|
| g (Erdbeschleunigung) | 9,81 m/s² |
| Vertikale Komponente bei Winkel α | cos(α) |
| Widerstand bei flachem Winkel | Belastung steigt erheblich bei α > 30° zur Vertikalen |
| Praktische Reserve | Herstellerangaben beachten; zusätzlich oft 10–25 % Sicherheitsaufschlag |
| Regelmäßige Inspektion | Vor jedem Einsatz Sichtkontrolle, jährliche Prüfung durch Fachkundigen |
Häufige Fehler und wie man sie vermeidet
Die klassischen Fehler sind immer wieder dieselben: zu flache Anschlagwinkel, Annahmen eines mittigen Schwerpunkts ohne Messung, Verwendung beschädigter Anschlagmittel, Unterschätzung dynamischer Effekte und mangelnde Kommunikation im Hebeteam. Vermeiden lassen sich diese Fehler durch systematisches Vorgehen: messen, skizzieren, rechnen, prüfen, testen.
Ein weiterer häufiger Fehler ist die unterschätzte Reaktion beim Verschieben eines schweren Teils während der Fahrt. Schon kleine seitliche Kräfte oder leichte Beschleunigungen können die Last umschlagen lassen, wenn das System nah an der Grenzbelastung arbeitet. Deshalb: immer Reserve einkalkulieren und nicht bis ans Limit gehen.
Software, Apps und digitale Hilfen
Für komplexe Hebeaufgaben gibt es spezialisierte Software und mobile Apps, die Hebeberechnungen, dynamische Simulationen und 3D-Ansichten erlauben. Diese Werkzeuge sind besonders nützlich bei langen Lasten, mehreren Hebepunkten oder komplizierter Geometrie. Sie ersetzen aber nicht das Verständnis der grundlegenden Prinzipien: lesen und prüfen Sie die Softwareergebnisse kritisch.
Vorteile digitaler Hilfen:
- Schnelle Lösung von Gleichungssystemen
- Visualisierung von Belastungspunkten
- Einbindung von Normen und Herstellerdaten
- Archivierung und Dokumentation von Hebevorgängen
Praxis-Tipps für den sicheren Hebevorgang
Ein paar praktische, leicht umsetzbare Empfehlungen helfen oft mehr als theoretische Perfektion:
– Hebepunkte markieren: Vor dem Ansetzen Hebepunkte sichtbar markieren.
– Langsam anheben: Erst kurz anheben, prüfen und korrigieren.
– Kommunikation: Klare Handzeichen oder Funk, nur eine verantwortliche Person gibt das Signal.
– Umgebung sichern: Keine Personen unter der Last, Hindernisse entfernen.
– Witterung beachten: Wind kann große Flächen destabilisieren.
– Probelasten: Bei Unsicherheit kurz anheben und Position kontrollieren.
Zusammenfassung der wichtigsten Formeln
– Gewichtskraft: W = m·g
– Schwerpunkt (x-Achse): x_CG = (Σ m_i·x_i) / Σ m_i
– Moment: M = F·d
– Zwei Hebepunkte (Abstände x1, x2 vom Schwerpunkt): T1 = W·x2/(x1+x2), T2 = W·x1/(x1+x2)
– Zwei symmetrische Schlingen mit Winkel α zur Vertikalen: T (pro Schlinge) = W / (2·cos(α))
Diese Formeln bilden die Grundlage für die meisten Hebeaufgaben. Wenn mehrere Hebepunkte, mehrere Achsen oder Schrägstellungen ins Spiel kommen, nutzt man dieselben Prinzipien in erweitertem algebraischem Rahmen.
Wenn Sie unsicher sind: Holen Sie Expertenrat
Keine Rechnung, keine Excel-Tabelle und kein Erfahrungswert ersetzt die Verantwortung eines Befähigten oder eines Tragwerksplaners bei kritischen Hebevorgängen. Bei besonders wertvollen, gefährlichen oder komplexen Lasten sollte immer ein qualifizierter Ingenieur hinzugezogen werden. Dokumentieren Sie Berechnungen, Freigaben und Prüfergebnisse – das schützt das Team und die Firma.
Schlussfolgerung
Die sichere Berechnung von Last und Schwerpunkt ist eine Kombination aus physikalischem Grundverständnis, sorgfältigem Messen und umsichtigem Planen. Mit einfachen Formeln, systematischen Schritten und der richtigen Ausrüstung können Sie die meisten Hebevorgänge sicher planen: Gewicht bestimmen, Schwerpunkt ermitteln, Hebepunkte wählen, Momentengleichgewichte lösen, Winkeleffekte beachten, Sicherheitsfaktoren anwenden und vor dem endgültigen Heben immer einen Testlauf machen. Bewahren Sie Vorsicht, dokumentieren Sie Ihre Berechnungen und verlassen Sie sich auf zertifizierte Ausrüstung und qualifiziertes Personal — so wird aus einer kritischen Hebeaufgabe eine kontrollierte und sichere Routine.